Indudablemente, los problemas de Deep Learning están cerca de ocupar el primer puesto entre los tópicos populares del mundo de la ciencia de datos hoy día, y con razón, por el tipo de tareas que se están intentando realizar con estas tecnologías.
Esta publicación pretende servir como guía de iniciación al deep learning con R. Al ser un post introductorio, se describiran los paquetes necesarios y la forma de instalarlos, se recomendará bibliografía para entender las redes neuronales y se realizará un ejercicio básico.
En la publicación La grandeza de Kobe Bryant I: Componentes principales se sentaron las bases para comprender el manejo de imágenes en R. El ejercicio aborda la forma de importar una imagen y la manera en la que el software representa estos objetos, entre otras cosas.
Esta vez el ejercicio es un poco más amplio, porque en lugar de manejar una sola imagen, se manipulará todo un array con miles de ellas, con la finalidad de construir un modelo de clasificación con las tecnologías actuales de deep learnig.
Tensorflow y keras
Tensorflow es un framework de machine learnig que facilita el acceso a una serie de algoritmos y modelos para tratar problemas modernos de clasificación y regresión como los de reconocimiento y clasificación de imágenes, procesamiento de lenguaje natural, forecast de series temporales y otros.
Así como otros frameworks de machine learning, tensorflow tiene una integración con python para proveer una interfaz de programación de aplicaciones (API por sus siglas en inglés), aunque las aplicaciones y operaciones se ejecutan finalmente en c++.
Por otra parte, Keras es un interfaz de deep learning para python, capaz de correr tanto sobre tensorflow como en el framework de microsoft, Microsoft Cognitive Toolkit.
Al decir que keras es un interfaz para estos frameworks de deep lerning, se apunta a que es una manera de acceder a las herramientas de tensorflow de una forma sencilla y reduciendo el riesgo de cometer errores.
De forma reducida, tensorflow es un framework de machine learning y keras en un API para tensorflow, desarrollada en python.
El punto es el siguiente, cuando vamos al mundo de R, tenemos el paquetes {keras}, que es a su vez una interfaz para el keras de python. Lo que quiere decir, que tenemos los beneficios de la programación en R mientras aprovechamos la capacidad de python.
La integración entre R y Python se da mediante el paquete {reticulate}. Pueden leer más detalles en la página web del paquete.
Instalando {tensorflow} y {keras}
El portal oficial de tensorflow para R creado por Rstudio provee una guía de instalación bastante clara, con una serie de pasos que se presentan a continuación
- Instalar el paquete
{tensorflow}coninstall.packages("tensorflow") - Instalar tensorflow con la función
tensorflow::install_tensorflow(). Para lograr esto es necesario tener una versión de Anaconda. - Luego instalar el paquete
kerasconinstall.packages("keras")
Si no tienes una versión de Anaconda instalada, al momento de tratar de instalar tensorflow, el software te dará la opción de instalar Miniconda (una versión sencilla del navegador con los componentes imprescindibles). Es decisión particular instalar Miniconda o descargar manualmente Ananconda.
La data
La data a utilizar esta vez viene siendo como el iris o mtcars del deep learnig. Se trata del set de datos mnist, una colección de imágenes de números escritos a mano con dimensión 28 x 28 pixeles. El paquete {keras} trae funciones para habilitar varios sets de datos, listos para entrenar modelos de deep learnig, entre ellos el mnist.
# Paquetes
library(keras)
library(tensorflow)
library(tidyverse)
# Mnist data set
mnist <- keras::dataset_mnist()Es importante que para este punto ya conozcan los arrays. Si no los conocen es recomendable leer la descripción que da Hadley Wickham en la sección 3.3.3 de su libro Advance R (la sección 4.2.3 también).
En general, tanto las matrices como los arrays son vectores, pero con un atributo adicional, la dimensión. Los vectores en su forma básica no tienen dimensión, son una simple coleción de elementos, aunque por convención la gente considera que son objetos de una dimensión.
my_vector <- 1:12
dim(my_vector)## NULLdim(my_vector) <- c(3, 4)
my_vector## [,1] [,2] [,3] [,4]
## [1,] 1 4 7 10
## [2,] 2 5 8 11
## [3,] 3 6 9 12dim(my_vector) <- c(2, 2, 3)
my_vector## , , 1
##
## [,1] [,2]
## [1,] 1 3
## [2,] 2 4
##
## , , 2
##
## [,1] [,2]
## [1,] 5 7
## [2,] 6 8
##
## , , 3
##
## [,1] [,2]
## [1,] 9 11
## [2,] 10 12Se trae esto a colación por la estructura en la que viene el set de datos mnist. Este objeto contiene dos listas mnist$train y mnist$test. Estas a su vez contienen dos elementos, 2 arrays, mnist$train$x con las imágenes y mnist$train$y con las etiquetas de cada una, o dicho de otra forma, el número que aparece en la imagen.
Es propicio decir que tanto en el train como el en test set, hay igual cantidad de imágenes y etiquetas, con una correspondencia de uno a uno.
Es importante saber manipular arrays por esta razón. A continuación, una forma de hacer un gráfico de las imágenes del set de datos.
# para hacer un grid 12 x 12 imageners
# 144 en total
imagenes <- 1:144
# Generando el grid de imágenes
imagenes %>%
# para iterar sobre las primeras n imagenes
map(
~mnist$train$x[.x, , ] %>%
#transformar a dataframe
as.data.frame() %>%
# agregar el ide de la columna
# para identificar la posición de cada pixel
rowid_to_column(var = "y") %>%
# reshape del dataframe
gather("x", "value", -y) %>%
# volviendo la variable x numerica
mutate(x = parse_number(x)) %>%
# gráfico de tiles
ggplot(aes(x = x, y = y, fill = value)) +
geom_tile(show.legend = FALSE) +
# reorganizando el eje y
scale_y_reverse() +
scale_fill_gradient(low = "white", high = "black") +
theme_void()
) %>%
cowplot::plot_grid(plotlist = .)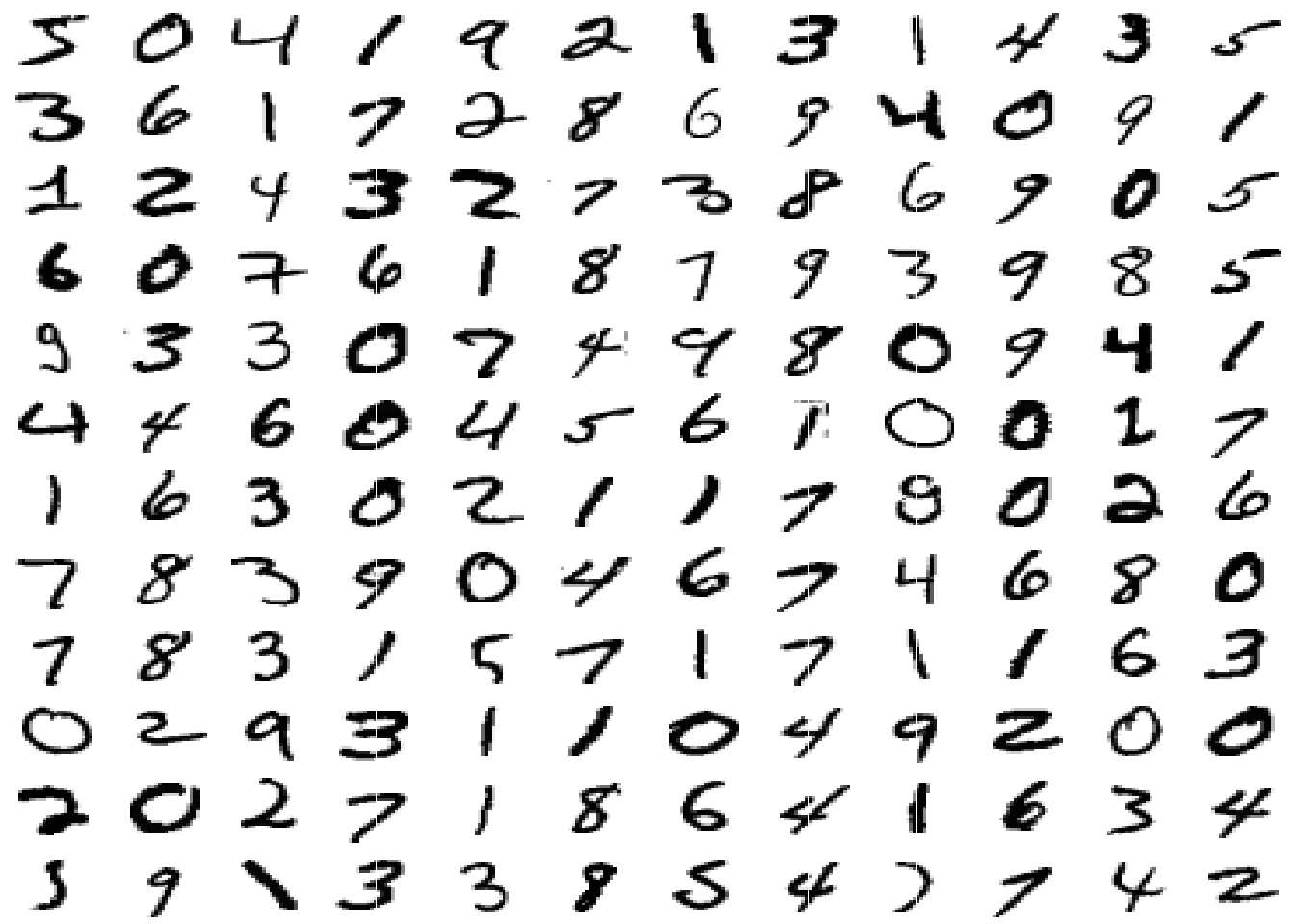
Neural Network, para luego
En este punto del post manda una breve explicación de las redes neuronales, pero no siento que he interiorizado los conceptos lo suficiente como para compartir un resumen con el que me sienta cómodo. En los próximos ejercicios dejaré mi versión, pero en esta simplemente comparto enlaces a artículos que a mi parecer hacen un buen trabajo capturando la intuición de la metodología.
- El capitulo 2 del libro Deep learning with R
- A Visual and Interactive Guide to the Basics of Neural Networks
- Entendiendo las redes neuronales PART 1
- Introducing Deep Learning and Neural Networks — Deep Learning for Rookies (1)
Hay muchos conceptos de por medio: capas, capas ocultas, nodos o neuronas, funciones de pérdida, optimizadores…
Clasificando las imágenes
Reescalar los datos
Las imágenes del set de datos vienen con pixeles en una intensidad entre 0 y 250, en este punto cambiamos a escara para acotarlos en valores entre 0 y 1.
# Cambiando la intensidad de los pixeles
# de una escala de 0 a 250 a una de 0 a 1
mnist$train$x <- mnist$train$x/255
mnist$test$x <- mnist$test$x/255Construyendo el modelo
La estructura de las redes neuronales se compone de capas, en las cuales se especifican elementos del imput, de las transformaciones que se le realizaran a los datos y otras capas cuyos parámetros se ajustan durante el entrenamiento.
En el caso del modelo que nos compete, la capa flatten recibe las dimensione que tiene cada imagen de entrenamiento, esto para cambiar la dimensión y pasarla de un array de dos dimensiones (28 * 28) a una dimensión de 784 elementos.
Luego se especifican dos capas dense, en la primera se establece la cantidad de nodos o neuronas de la red y la función de activación. En este caso se usa una de las más comunes, la función de activación ReLU.
En la segunda capa dense, la capa del output, se especifican los nodos de salida, uno por cada categoría probable, y al tratarse de números del 0 al 9 se especifican 10, El segundo argumento de esta capa hace que el resultado del modelo sea un array con 10 valores de probabilidad que suma uno. En este caso el nodo de la categoría que tenga el mayor score termina siendo la predicción.
La última capa es la dropout, que especifica una cantidad de neuronas que serán desactivas aleatoriamente durante el período de entrenamiento. Esta es una práctica común en muchos algoritmos de machine learning, en el Random Forest, por ejemplo, los árboles se entrenan con una selección aleatoria de variables explicativas.
model <- keras_model_sequential() %>%
layer_flatten(input_shape = c(28, 28)) %>%
layer_dense(units = 128, activation = "relu") %>%
layer_dropout(0.2) %>%
layer_dense(10, activation = "softmax")Para inspeccionar el modelo se puede utilizar la función summary (Esta función tiene métodos para todos los objetos).
summary(model)## Model: "sequential"
## ________________________________________________________________________________
## Layer (type) Output Shape Param #
## ================================================================================
## flatten (Flatten) (None, 784) 0
##
## dense_1 (Dense) (None, 128) 100480
##
## dropout (Dropout) (None, 128) 0
##
## dense (Dense) (None, 10) 1290
##
## ================================================================================
## Total params: 101,770
## Trainable params: 101,770
## Non-trainable params: 0
## ________________________________________________________________________________Compilando el modelo
El siguiente paso es compilar el modelo. En este punto se especifican los siguientes elementos.
Función de pérdida: establece cómo la red neuronal irá midiendo su rendimiento durante el entrenamiento. La suma cuadrada de residuos es una función de pérdida muy común, se utiliza en metodologías más tradicionales como las regresiones lineales. La idea de los algoritmos que usan esa función de pérdida es minimizarla.
Optimizador: es el mecanismo mediante el cual la red se retroalimenta a sí misma durante el entrenamiento. De estos hay varios, pero el adam es de los más comunes.
Métrica: especifíca a que se le va a presentar atención durante el entrenamiento del modelo. En este caso al accuracy, o bien la proporción de imágenes bien clasificadas.
model %>%
compile(
loss = "sparse_categorical_crossentropy",
optimizer = "adam",
metrics = "accuracy"
)Entrenando el modelo
La función fit() tiene dos argumentos esenciales, las imágenes o imputs en el argumento x, y los labels de cada uno como y.
Otro elemento es epoch, que indica la cantidad de iteraciones que hará el modelo para entrenarse. Cada iteración se realiza sobre el set de entrenamiento completo.
El argumento verbose permite controlar que indicadores de progreso desplegará el modelo mientras se entrena. Para una entrada de blog como esta se coloca un dos para que el log sea más reducido. Así simplemente se despliegan los resultados generales para cada iteración.
En la documentación del paquete kera, el Python, está la descripción detallada de cada argumento, tanto de la función fit() como de compile(). Para leer con más detalles acceder con este enlace
model %>%
fit(
x = mnist$train$x, y = mnist$train$y,
epochs = 5,
validation_split = 0.3,
verbose = 2
)history <- model %>%
fit(
x = mnist$train$x, y = mnist$train$y,
epochs = 5,
validation_split = 0.3,
verbose = 2
)En un gráfico también se puede apreciar la evolución de los indicadores del modelo durante el entrenamiento. El resultado muestra el comportamiento esperado, la función de pérdida disminuyendo en cada iteración y el accuracy o proporción de imagenes bien clasificadas en aumento.
Como ven hay dos líneas, esto porque en cada iteración el set de entrenamiento se divide y una parte de los datos se usa para entrenar el modelo y otra para probarlo. Para eso se usó el parámetro validation_split = 0.3 (30% de la data se usa para validación).
plot(history) +
geom_line() +
labs(x = "Iteración",
color = "Data",
title = "Desempeño del modelo durante el entrenamiento") +
theme_light() +
theme(legend.position = "bottom")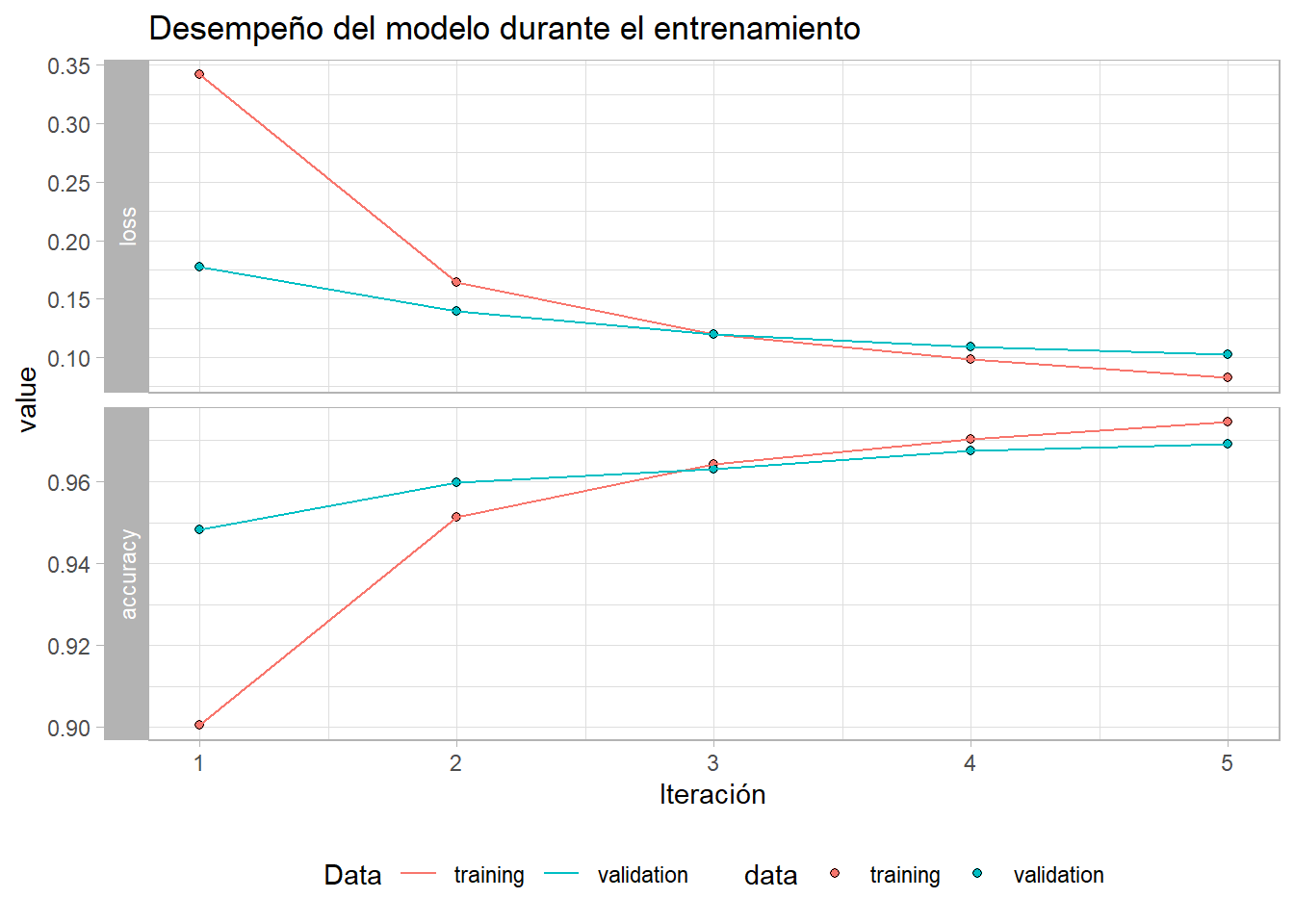
Probando el modelo con el test set
Teniendo ya el modelo entrenado, se usa la función predict() y una serie de imágenes no utilizadas para entrenar el modelo para probar su desempeño fuera de muestra. Este paso es crucial, porque de registrar aquí un desempeño muy por debajo del obtenido con el training set, entonces estaríamos frente a un problema de overfitting. En otras palabras, el modelo solo funciona con los datos que conoce.
Para hacer las predicciones hay varias opciones, con diferentes outputs cada una. En este caso se usa la función predict_classes(), que devuelve la clase que sugiere el modelo para cada observación del test set. Por otro lado, la función predict_prob() devuelve un array con el score de probabilidad de las potenciales clases para cada observación.
Obviamente, la clase con el escore de probabilidad mayor es la que se utiliza como output en predict_classes().
predictions <- model %>% predict(mnist$test$x)
head(predictions, 10)## [,1] [,2] [,3] [,4] [,5]
## [1,] 7.094636e-08 6.201533e-08 1.054558e-05 4.571944e-04 2.161721e-11
## [2,] 3.677354e-08 5.961317e-06 9.999627e-01 1.412775e-05 4.655819e-14
## [3,] 1.727000e-06 9.980060e-01 2.364296e-04 2.762344e-05 1.542673e-04
## [4,] 9.999428e-01 4.145325e-09 5.058305e-06 7.175230e-07 1.169020e-07
## [5,] 8.193841e-07 3.286226e-09 1.378264e-05 8.060075e-08 9.930353e-01
## [6,] 2.352434e-08 9.995110e-01 1.947651e-06 6.341837e-07 6.313050e-06
## [7,] 2.788663e-09 2.615654e-08 2.741148e-06 3.636903e-06 9.956767e-01
## [8,] 5.093751e-07 3.175913e-06 3.660624e-04 2.505129e-03 5.362818e-03
## [9,] 1.555835e-06 3.758887e-06 2.924458e-03 1.832690e-06 6.260694e-06
## [10,] 2.028173e-10 3.945598e-12 1.406860e-08 6.559767e-06 7.383234e-04
## [,6] [,7] [,8] [,9] [,10]
## [1,] 1.449906e-07 1.912452e-11 9.995291e-01 5.360926e-07 2.266261e-06
## [2,] 1.680496e-05 2.022807e-07 7.807416e-14 1.438396e-07 4.461754e-14
## [3,] 3.465242e-06 1.526870e-05 1.436348e-03 1.145453e-04 4.319025e-06
## [4,] 1.318318e-05 3.101458e-05 6.240952e-06 4.242222e-08 8.392549e-07
## [5,] 5.679764e-07 4.206001e-06 3.464545e-04 3.036828e-06 6.595771e-03
## [6,] 1.485579e-08 5.532178e-08 4.755452e-04 4.051059e-06 4.621940e-07
## [7,] 5.611032e-04 5.398598e-07 2.963992e-04 9.332893e-04 2.525528e-03
## [8,] 2.613762e-05 3.282717e-08 6.427758e-04 3.787016e-05 9.910554e-01
## [9,] 6.494704e-01 3.473006e-01 7.421287e-09 2.669928e-04 2.405662e-05
## [10,] 9.213137e-09 2.603555e-10 1.323996e-03 1.802063e-06 9.979293e-01Comprobando el desempeño del modelo
Finalmente se comprueba el desempeño general del modelo. En este caso un porcentaje de acierto que ronda el 98%, con el set de prueba. La verdad es que la mayoría de ejemplos consultados obtienen un mejor desempeño, con un 80 no se pasa la prueba, y por tanto tocará afinar un poco mejor la construcción del modelo.
model %>%
evaluate(mnist$test$x, mnist$test$y, verbose = 0)## loss accuracy
## 0.08933673 0.97259998Comentarios finales
Con esto se cubre el objetivo inicial, pero quedan muchas cosas por delante. Por tanto, la recomendación final es continuar leyendo y buscando conenido bien estructurado. El libro de François Chollet cumple este requerimiento, al igual este curso en data camp y sus prerequisitos.
Referencias
- keras: Deep Learning in R, Karlijn Willems
- A Visual and Interactive Guide to the Basics of Neural Networks, Jay Alammar
- Introducing Deep Learning and Neural Networks — Deep Learning for Rookies (1), Nahua Kang
- Basic Image Classification, Rstudio
- tensorflow with r overview, Rstudio
- Deep Learning with R, François Chollet & J. J. Allaire
- Keras documentation
- Advance R, Hadley Wickham
comments powered by Disqus